Допуски формы и расположения. Допуски расположения Отклонение от параллельности осей

Любая технологическая операция может быть выполнена с определенной точностью, а значит размеры полученной в результате обработки детали не будут идеальными, они могут колебаться в некотором диапазоне. Для того, чтобы выполнить условия собираемости и обеспечить надежную работу детали в заданных условиях необходимо задать допустимый интервал, в который должен попасть итоговый размер. Этот интервал может регламентировать не только линейные или диаметральные размеры, но и форму или взаимное расположение поверхностей.

Допуски формы и расположения назначаются конструктором исходя из условий сборки и особенностей работы детали в механизме.

Виды допусков формы

Допуском формы называют максимальное допускаемое значение отклонения формы.

Поле допуска формы - это область на плоскости или в пространстве, внутри которой должны находиться все точки рассматриваемого элемента в пределах нормируемого участка, ширина или диаметр которой определяется значением допуска, а расположение относительно реального элемента прилегающим элементом.

Отклонения и допуски формы

Различают следующие допуски на отклонения формы:

• Отклонение от прямолинейности в плоскости
• выпуклость
• вогнутость
• Отклонение от плоскости и допус плоскостности
• Выпуклость
• Вогнутость
• Отклонение от круглости и допуск круглости
• Овальность
• Огранка
• Отклонение от цилиндричности и допуск цилиндричности
• Отклонение и допуск профиля продольного сечения цилиндрической поверхности
• Отклонение профиля продольного сечения
• Конусообразность
• Бочкообразность
• Седлообразность

Допустимые отклонения обозначаются специальными символами.

Виды допусков расположения

Допуск расположения - предел, ограничивающий допускаемое значение отклонения расположения.

Различают допуски месторасположения и допуски ориентации.

Поле допуска расположения - область на плоскости или в пространстве, внутри которой должен находиться прилегающий элемент или плоскость симметрии, ось, центр в пределах нормируемого участка, диаметр или ширина которой определяется значение допуска, а расположение относительно - номинальным расположением рассматриваемого элемента.

Отклонения и допуски расположения

Различают следующие виды допусков расположения:

• Отклонение от параллельности и допуск параллельности
• Отклонение и допуск перпендикулярности
• Отклонение и допуск наклона
• Отклонение и допуск соосности
• Допуск в радиусном выражении
• Отклонение и допуск симметричности
• Позиционное отклонение и позиционный допуск
• Допуск в диаметральном выражении
• Допуск в радиусном выражении
• Отклонение от пересечения и допуск пересечения осей
• Допуск в диаметральном выражении
• Допуск в радиусном выражении

Суммарные допуски

Существует несколько видов суммарных допусков формы и расположения.

• Радиальное биение
• Полное радиальное биение
• Торцовое биение
• Полное торцовое биение
• Биение в заданном направлении
• Отклонение и допуск формы заданного профиля
• Отклонение и допуск формы заданной поверхности

Эти допуски обозначаются символами.

Обозначение допусков формы и расположения на чертежах

Допуски формы и расположения изображают на чертежах в виде рамки, которая поделена на несколько частей. В первой части изображают графическое обозначение допуска, во второй части - числовое значение допуска, в третей и последующий - буквенное обозначение одной или нескольких баз.

В случае отсутствия базы допуска рамка состоит только из двух частей. Примеры рамок допусков формы и расположения показаны на рисунке.

На рисунке слева показана рамка с допуском формы (допустимое отклонение от прямолинейности), справа с допуском расположения (допустимое отклонение от параллельности).

Рамку выполняют тонкими линиями. Высота текста в рамке должна равняться размеру шрифта размерных чисел. От рамки допуска до поверхности или до выноски проводится линия, оканчивающаяся стрелкой.

Перед числовым значение допуска могут указываться знаки:

• ф - если цилиндрическое или круговое поле допуска указываются диаметром
• R - если цилиндрическое или круговое поле указываются радиусом
• Т - если поле допуска пересечения осей, симметричности, ограничены двумя параллельными прямыми или плоскостями в диаметральном выражении.
• Т/2 - в том же случае, что и Т, только в радиусном выражении
• Сфера - для шарового поля допуска.

Если допуск должен применяться не ко всей поверхности, а только к некоторому участку, то он обозначается штрих пунктирной линией.

Для одного элемента может быть указано несколько допусков, этом случае рамки изображаются одна над другой.

Дополнительная информация может быть указана над рамкой или под ней.

Информация о допусках формы и расположения может быть указана в .

Неуказанные допуски соосности по ГОСТ 25069-81.

Зависимые допуски

Зависимые допуски расположения обозначают следующим символом .

Этот символ может быть размещен после числового значения допуска, если зависимый допуск связан с действительными размерами рассматриваемого элемента. Также символ может быть размещен после буквенного обозначение (если оно отсутствует то в третьем поле рамки) в том случае, если зависимый допуск связан с действительными размерами базового элемента.

Назначение допусков формы и расположения

Чем точнее изготовлена деталь, тем более точные инструменты потребуются для ее изготовления и контроля размеров. Это автоматически увеличит ее стоимость. Получается, что цена изготовления детали во многом зависит от требуемой точности при ее изготовлении. Это означает, что конструктор должен указать лишь те допуски, которые действительно необходимы для сборки и надежной работы механизма. Допустимые интервалы также должны быть назначены исходя из условий собираемости и работоспособности.

Числовые значения допусков формы

В зависимости от класса точности устанавливаются стандартные значения допусков формы.

Допуски плоскостности и прямолинейности

Номинальным размеров в данном случае считается номинальная длина нормированного участка.

Допуски круглости, цилиндричности, профиля продольного сечения

Данные допуски назначаются в тех случаях, когда они должны быть меньше, чем допуск размера.

Номинальным размером считается номинальный диаметр поверхности.

Допуски перпендикулярности, параллельности, наклона, торцевого биения

Номинальным размером при назначении допусков на параллельность, перпендикулярность, наклон понимается номинальная нормируемого участка или номинальная длина всей контролируемой поверхности.

Допуски радиального биения, симметричности, соосности пересечения осей в диаметральном выражении

При назначении допусков радиального биения номинальным размером считается номинальный диаметр рассматриваемой поверхности.

В случае назначения допусков симметричности, пересечения осе соосности номинальным размером считается номинальный диаметр поверхности или номинальный размер между поверхностями, которые образуют рассматриваемый элемент.

Две плоскости в пространстве могут быть параллельными или могут пересекаться, как показано в следующей таблице.

Две пересекающиеся плоскости

Определение: Две плоскости называют пересекающимися , если они не совпадают , и у них есть общие точки . В случае, когда две плоскости пересекаются, пересечением этих плоскостей является прямая линия .

Две параллельные плоскости

Определение: Две плоскости называют параллельными , если они не имеют общих точек .

Признаки параллельности двух плоскостей

Первый признак параллельности двух плоскостей . Если две пересекающиеся прямые пересекающиеся прямые , лежащие в одной плоскости, соответственно параллельны параллельны двум прямым, лежащим в другой плоскости, то такие плоскости параллельны.

Доказательство . Рассмотрим рисунок 1, на котором изображены плоскости α и β

Прямые a и b лежат в плоскости α и пересекаются в точке K . Прямые c и d лежат в плоскости β и параллельны прямым a и b соответственно.

Будем доказывать первый признак параллельности двух плоскостей методом «от противного». Для этого предположим, что плоскости α и β не параллельны. Следовательно, плоскости α и β должны пересекаться, причём пересекаться по некоторой прямой. Обозначим прямую линию, по которой пересекаются плоскости α и β буквой l (рис.2) и воспользуемся признаком параллельности прямой и плоскости .

Плоскость α проходит через прямую a , параллельную прямой c , и пересекает плоскость β по прямой l . Отсюда, в силу , заключаем, что прямые a и l параллельны. В то же время плоскость α проходит через прямую b , параллельную прямой d , и пересекает плоскость β по прямой l . Отсюда, в силу признака параллельности прямой и плоскости , заключаем, что прямые b и l параллельны. Таким образом, мы получили, что на плоскости α через точку K проходят две прямые, а именно, прямые a и b , которые параллельны прямой l . Полученное противоречие с аксиомой о параллельных прямых даёт возможность утверждать, что предположение о том, что плоскости α и β пересекаются, является неверным. Доказательство первого признака параллельности двух плоскостей завершено.

Второй признак параллельности двух плоскостей . Если две пересекающиеся прямые, лежащие в одной плоскости, параллельны другой плоскости, то такие плоскости параллельны.

Доказательство . Рассмотрим рисунок 3, на котором изображены плоскости α и β .

На этом рисунке также изображены прямые a и b , которые лежат в плоскости α и пересекаются в точке K. По условию каждая из прямых a и b параллельна плоскости β . Требуется доказать, что плоскости α и β параллельны.

Доказательство этого утверждения аналогично доказательству первого признака параллельности двух плоскостей, и мы его оставляем читателю в качестве полезного упражнения.

На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике .

индивидуальные занятия с репетиторами по математике и русскому языку

Параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
Доказательство. Пусть a и b - данные плоскости, а 1 и а 2 – прямые в плоскости a , пересекающиеся в точке А , b 1 и b 2 соответственно параллельные им прямые в плоскости b . Допустим, что плоскости a и b не параллельны, то есть они пересекаются по некоторой прямой с . Прямая а 1 параллельна прямой b 1 , значит она параллельна и самой плоскости b (признак параллельности прямой и плоскости). Прямая а 2 параллельна прямой b 2 , значит она параллельна и самой плоскости b (признак параллельности прямой и плоскости). Прямая с принадлежит плоскости a , значит хотя бы одна из прямых а 1 или а 2 пересекает прямую с, то есть имеет с ней общую точку. Но прямая с также принадлежит и плоскости b , значит, пересекая прямую с, прямая а 1 или а 2 пересекает плоскость b , чего быть не может, так как прямые а 1 и а 2 параллельны плоскости b . Из этого следует, что плоскости a и b не пересекаются, то есть они параллельны.

Теорема 1 . Если две параллельные плоскости пересекаются третей, то прямые пересечения параллельны.
Доказательство. Пусть a и b - параллельные плоскости, а g - плоскость, пересекающая их. Плоскость a пересеклась с плоскостью g по прямой а. Плоскость b пересеклась с плоскостью g по прямой b . Линии пересечения а и b лежатв одной плоскости g и потому могут быть либо пересекающимися, либо параллельными прямыми. Но, принадлежа двум параллельным плоскостям, они не могут иметь общих точек. Следовательно, они параллельны.

Теорема 2. Отрезки параллельных прямых, заключенных между двумя параллельными плоскостями, равны.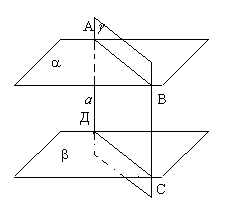
Доказательство. Пусть a и b - параллельные плоскости, а а и b – параллельные прямые, пересекающие их. Через прямые а и b проведем плоскость g (эти прямые параллельны, значит определяют плоскость, причем только одну). Плоскость a пересеклась с плоскостью g по прямой АВ. Плоскость b пересеклась с плоскостью g по прямой СД.По предыдущей теореме прямая с параллельна прямой d . Прямые а, b , АВ и СД принадлежат плоскости g .Четырехугольник, ограниченный этими прямыми,есть параллелограмм (у него противоположные стороны параллельны). А раз это параллелограмм, то противоположные стороны у него равны, то есть АД = ВС

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

Введем понятие параллельных плоскостей

Согласно аксиоме A3, если две плоскости имеют общую точку, то они пересекаются по прямой.

Отсюда следует, что плоскости либо пересекаются по прямой, либо не пересекаются, т. е. не имеют ни одной общей точку.

Определение. Две плоскости называются параллельными, если они не пересекаются.

Если плоскости параллельны, пишут: .

Теорема (признак параллельности плоскостей).

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

Доказательство.

Рассмотрим две плоскости: .

В плоскости лежат пересекающиеся прямые a1 и b1, а в плоскости параллельные им пересекающиеся прямые a2и b2.

Докажем, что.

Доказательство. Рассуждаем методом от противного.

Предположим, что плоскости не параллельны. Тогда существует прямая c, по некоторой они пересекаются.

Так как прямая a1 параллельна прямой a2 , лежащей в плоскости, то прямая a1 параллельна плоскости.

Аналогично, прямая b1 параллельна плоскоcти.

Теперь можно воспользоваться свойством прямой, параллельной плоскости.

Так как плоскость проходит через прямую a1, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей c будет параллельна прямой a1, т.е.

Но плоскость проходит и через прямую b1, параллельную плоскости, поэтому.

Таким образом, через точку O1 проходят две прямые a1 и b1 , параллельные прямой c.

Но это невозможно, через O1 может проходить только одна прямая, параллельная с.

Предположив, что мы пришли к противоречию. Следовательно, .

Теорема доказана.

Задача 1. Три отрезка A1A2, B1B2 и C1C2, не лежащие в одной плоскости, имеют общую середину. Докажите, что плоскости A1B1C1 и A2B2C2 параллельны.

Отрезки A1A2, B1B2 и C1C2 не лежат в одной плоскости

O - общая середина отрезков

Доказать: Плоскость A1B1C1 плоскости A2B2C2

В плоскости A1B1C1возьмем пересекающиеся отрезки A1B1 и A1C1 , а в плоскости A2B2C2 - отрезки A2B2 и A2C2. Докажем, что они соответственно параллельны.

Рассмотрим четырехугольник A1B1A2B2.

Так как его диагонали в точке пересечения делятся пополам, то это параллелограмм.

Поэтому A1B1 A2B2

Аналогично из четырехугольника A1C1A2C2 получим, что A1C1 A2C2.

По признаку параллельности плоскостей,

На этом уроке мы дадим определение параллельных плоскостей и вспомним аксиому о пересечении двух плоскостей. Далее мы докажем теорему - признак параллельности плоскостей и, опираясь на нее, решим несколько задач на параллельность плоскостей.

Тема: Параллельность прямых и плоскостей

Урок: Параллельные плоскости

На этом уроке мы дадим определение параллельных плоскостей и вспомним аксиому о пересечении двух плоскостей.

Определение. Две плоскости называются параллельными, если они не пересекаются.

Обозначение : .

Иллюстрация параллельных плоскостей (Рис. 1.)

1. Какие плоскости называются параллельными?

2. Могут ли быть параллельными плоскости, проходящие через непараллельные прямые?

3. Каким может быть взаимное расположение двух прямых, каждая из которых лежит в одной из двух различных параллельных плоскостей?

4. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. - 5-е издание, исправленное и дополненное - М.: Мнемозина, 2008. - 288 с.: ил.

Задания 1, 2, 5 стр. 29